| Neuronales
Netz |
|
Kurzbeschreibung |
Lernfunktion: Der Trick liegt darin, ein gewünschtes Ergebnis
zu definieren und das System selbst experimentieren zu lassen über
welche Wege (x) und mit welchen Gewichtungen (w) dieses Ergebnis erreicht
werden kann. Zumeist sind mehrere Lösungswege möglich. |
|
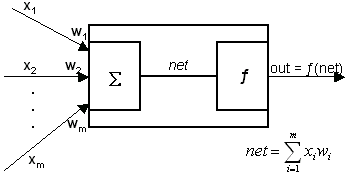
Neuronale Netze bestehen aus Knoten, den Neuronen. Solch ein
Elementarteil ist links dargestellt und unten beschrieben. Ein Netz entsteht
durch Verknüpfung des Ausgangs eines Knotens mit Eingängen
mehrerer anderer Neuronen.
-
x Eingabewerte
xi mit i=1...m sind die Eingabewerte.
-
w Netzgewicht
Jedem Eingang ist ein Netzgewicht wi zugeordnet.
-
net Netzaktivität
-
ƒ(net) Aktivierungsfunktion
ƒ(net) wird häufig als Schwellwert oder Treppenfunktion implementiert.
|
Beispiel:
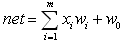und out = +1 falls net > 0, sonst –1 |
|
-
Linkes Beispiel zeigt ein Adaline / Madaline.
Die Schwellwerte w0..wi werden gelernt.
|
Sigmoidfunktion:
|
|
-
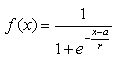
ƒ(net) kann auch durch die Sigmoidfunktion berechnet werden wobei a die
Lage des Durchgangs durch das Niveau 0.5 bestimmt und
r die Steigung der Sigmoidfunktion ist.
|
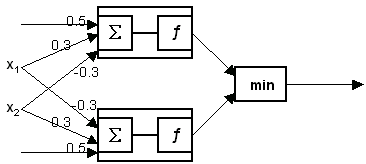
XOR Beispiel
|
|
Beispiel: XOR Funktionalität mit einem Mandaline
Anstatt der min Funktion können Mehrheit-, Einstimmigkeit-, Singulärverfahren
verwendet werden.
| x1 |
x2 |
f_oben |
f_unten |
out |
| 0 |
0 |
.3*0-.3*0+.5=.5 |
-.3*0+.3*0+.5=.5 |
0.5 |
| 0 |
1 |
.3*0-.3*1+.5=.2 |
-.3*0+.3*1+.5=.8 |
0.2 |
| 1 |
0 |
3*1-.3*0+.5=.8 |
-.3*1+.3*0+.5=.2 |
0.2 |
| 1 |
1 |
.3*1-.3*1+.5=.5 |
-.3*1+.3*1+.5=.5 |
0.5 |
|
|
|
